本篇示範如何使用 Google 的 TensorFlow、softmax 迴歸模型、CNN,實作一套手寫辨識系統。
如果您沒學過 Google 的 TensorFlow,建議先閱讀 TensorFlow 機器學習軟體工具入門教學。
本篇教學會以 MNIST 手寫影像資料作為範例,先以最簡單的 softmax 迴歸模型建立一個手寫辨識系統,準確率大約是 92%,接著再改用較為複雜的 CNN 模型,建立另外一個準確率更高的手寫辨識系統,最後的模型準確率可達 99%。
MNIST 手寫影像資料
MNIST 是一個手寫影像的測試資料集,包含了 60,000 筆訓練用資料,以及 10,000 筆測試用資料。
因為 TensorFlow 本身的內建範例就已經把資料的下載與讀取程式包裝好了,如果您只是想要嘗試跑一下 TensorFlow 的範例程式,可以直接跳過這段下載資料的步驟,這裡是敘述比較底層的 MNIST 資料格式,對於需要自己開發手寫程式的人才會比較需要了解。
下載 MNIST 手寫圖檔資料,總共有四的壓縮檔,分別為訓練用(training set)與測試用(test set)的影像與標示(label)檔:
# training set images (9912422 bytes) wget http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz # training set labels (28881 bytes) wget http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz # test set images (1648877 bytes) wget http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz # test set labels (4542 bytes) wget http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz
MNIST 的原始圖檔資料是 20×20 像素的手寫圖,計算重心之後,放在 28×28 的圖檔中心(重心對準新圖檔中心),而 training set 標示檔的檔案格式如下:
| Offset | 資料類型 | 資料值 | 說明 |
|---|---|---|---|
0000 |
32 bits integer | 0x00000801(2049) | magic number (MSB first) |
0004 |
32 bits integer | 60000 | 資料筆數 |
0008 |
unsigned byte | 0 ~ 9 |
label 資料 |
0009 |
unsigned byte | 0 ~ 9 |
label 資料 |
... |
unsigned byte | 0 ~ 9 |
label 資料 |
標示資料的值皆為 0 到 9 的數值。
training set 圖檔的檔案格式如下:
| Offset | 資料類型 | 資料值 | 說明 |
|---|---|---|---|
0000 |
32 bits integer | 0x00000803(2051) | magic number |
0004 |
32 bits integer | 60000 | 資料筆數 |
0008 |
32 bits integer | 28 | rows 數目 |
00012 |
32 bits integer | 28 | columns 數目 |
0016 |
unsigned byte | 像素資料 | |
0017 |
unsigned byte | 像素資料 | |
... |
unsigned byte | 像素資料 |
像素資料是採用 row-wise 的方式儲存的,其值為 0 到 255,0 代表背景(白色),255 代表前景(黑色)。
測試用資料集的資料格式也是類似,詳細的說明請參考 MNIST 的官方網頁說明。
下載四個壓縮檔之後,我們使用 gzip 解壓縮:
gzip -d *.gz
再用 od 查看一下這些二進位的檔案內容,例如:
od -t x1 -N 64 train-labels-idx1-ubyte
0000000 00 00 08 01 00 00 ea 60 05 00 04 01 09 02 01 03 0000020 01 04 03 05 03 06 01 07 02 08 06 09 04 00 09 01 0000040 01 02 04 03 02 07 03 08 06 09 00 05 06 00 07 06 0000060 01 08 07 09 03 09 08 05 09 03 03 00 07 04 09 08
準備 MNIST 資料
使用 TensorFlow 內建的教學程式碼,自動下載與讀取 MNIST 的資料:
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
將 MNIST 資料讀取進來之後,會分成三部份:
mnist.train:訓練用資料 55,000 筆。mnist.validation:驗證用資料 5,000 筆。mnist.test:測試用資料 10,000 筆。
每部份的資料都會有影像(例如 mnist.train.images)與標示(例如 mnist.train.labels),在這個手寫辨識的問題上,我們會將影像當作模型輸入的 x,而標示則當作模型輸出的 y。
這裡我們將每一個手寫數字的影像都視為長度為 28 * 28 = 784 的向量(其降維的研究可參考 colah’s blog),因此 mnist.train.images 就是一個 shape 為 [55000, 784] 的 tensor,其中每個數值都是一個介於 0 與 1 的浮點數。
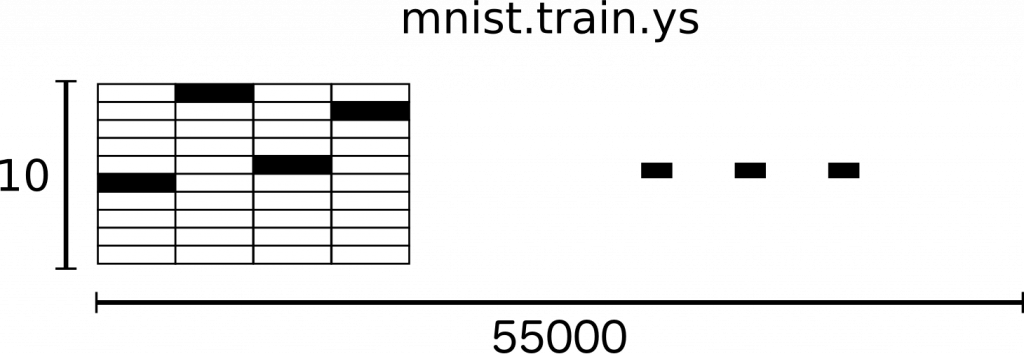
在標示的資料(mnist.train.label)上,我們使用長度為 10 的向量來表示 0 到 9 的數字,這種向量之中只有一個元素是 1,其餘都是 0,當第 n 個向量元素是 1 時就代表第 n 個數字,例如 [0, 0, 0, 1, 0, 0, 0, 0, 0, 0] 就代表 3,像這種向量就稱為 one-hot 向量。
Softmax 迴歸分析
在手寫數字辨識系統中,由於數字只有 0 到 9 這十種可能,當我們拿到一個手寫數字的影像時,我們的模型可能會認為這個影像有 80% 的機率是 9,而有 5% 的機率是 8,然後還有一些更小的機率是其他的數字。
Softmax 迴歸模型可以產生每一個結果的發生機率,而所有的發生機率總和為 1,像這種數字辨識問題就很適合使用 softmax 迴歸模型來處理,事實上在更複雜的分析模型中,也很常在最後的分析步驟上加上 softmax 迴歸模型來輸出機率值。
Softmax 迴歸分析有兩個步驟,第一步是針對某一個類別,加總所有的可能是此類別的表徵特性(evidence),第二步則是將這些表徵特性轉換為機率值。
給定一個手寫影像 (x),其會屬於第 (i) 個類別的表徵特性模型為:
[text{evidence}_i = sum_j W_{i,~ j} x_j + b_i]
其中 (W_{i,~ j}) 是權重(weight),(b_i) 是偏差值(bias),而 (x_j) 就是 (x) 的第 (j) 個像素值。
接著再將表徵特性經過 softmax 函數轉換為機率值 (y):
[y = text{softmax}(text{evidence})]
而 softmax 函數可以想像成一個標準化的函數:
[text{softmax}(x) = text{normalize}(exp(x))]
寫成實際的數學式就會像這樣:
[text{softmax}(x)_i = frac{exp(x_i)}{sum_j exp(x_j)}]
softmax 函數的指數函數會將 (x) 的線性差異轉為指數差異,關於這個函數的性質可參考 Michael Nielsen 的網頁。
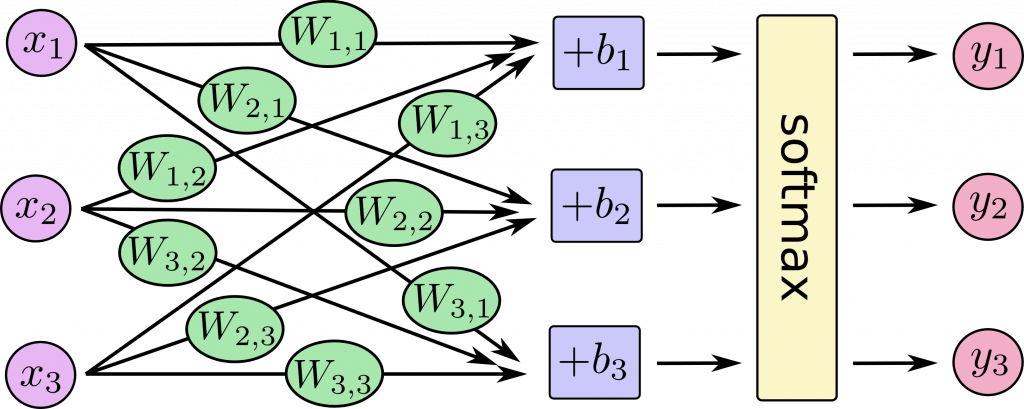
下圖是 softmax 回歸模型的示意圖,這裡以三個輸入的 (x_i)(三個像素)與三個輸出 (y)(三個數字的機率)作為示範:
若將此模型用方程式的寫法則為:
我們可以將上面的方程式,改為矩陣與向量運算的寫法:
最後用標準的數學式表示就是:
[y = text{softmax}(Wx + b)]
TensorFlow 實作
匯入 tensorflow 模組:
import tensorflow as tf
定義模型
定義模型,首先定義輸入的資料 x,:
x = tf.placeholder(tf.float32, [None, 784])
這裡的 x 就是多張 MNIST 的影像資料,每一張影像就是一個 784 維的向量,此處的 None 代表該維度的長度可以是任意值。
接著定義權重與偏差值:
W = tf.Variable(tf.zeros([784, 10])) b = tf.Variable(tf.zeros([10]))
由於 W 要乘上 784 維的向量(輸入影像),然後產生 10 維的表徵特性向量(代表一個數字),所以 W 的 shape 會是 [784, 10],而 b 只是單純加在 10 維的表徵特性向量上的常數而已,所以 shape 為 [10]。
建立主要的模型:
y = tf.nn.softmax(tf.matmul(x, W) + b)
此處我們使用 tf.matmul 處理矩陣乘法,再用 tf.nn.softmax 處理 softmax 函數。因為這裡的 x 從原本的一張影像變成了多張影像,也就是說 x 從向量變成了矩陣,所以為了計算方便,我們改成這樣寫,雖然它跟上面理論推導的數學式子不太一樣,但概念是不變的。
訓練模型
這裡我們使用 cross-entropy 的方式來衡量模型的表現,cross-entropy 函數的定義如下:
[H_{y’}(y) = -sum_i y’_i log(y_i)]
其中 (y) 是模型預測出來的機率分佈,而 (y’) 則是真實的分佈(對應的 one-hot 向量),這個值越小則代表模型表現越好,也就是模型預測結果越接近真實的分佈。關於 cross-entropy 的理論請參考 colah’s blog 的文章。
在實作 cross-entropy 時,我們要增加一個 placeholder 來輸入真實的分佈(正確答案):
y_ = tf.placeholder(tf.float32, [None, 10])
接著實作 cross-entropy 函數:
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1]))
這裡先用 tf.log 計算每個 (y) 元素的 (log) 轉換,再以元素對元素(一對一對應)的方式乘以 y_,然後使用 tf.reduce_sum 配合 reduction_indices=[1] 參數,將這個矩陣沿著第二維度加總,最後再使用 tf.reduce_mean 計算整個向量的平均值。
由於這行程式碼在數值計算上不穩定,在實際使用上,我們會改用 tf.nn.softmax_cross_entropy_with_logits 這個函數來計算。
cross_entropy = tf.reduce_mean( tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y))
接著使用 backpropagation 演算法尋找最佳解:
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)
這裡我們使用 gradient descent 演算法,learning rate 取 0.5。TensorFlow 本身還有提供其他許多的 optimizer 可以使用,請參考 TensorFlow 的文件。
建立一個 InteractiveSession,並初始化 variables:
sess = tf.InteractiveSession() tf.global_variables_initializer().run()
進行 1000 次的訓練:
for _ in range(1000): batch_xs, batch_ys = mnist.train.next_batch(100) sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})
我們使用 stochastic gradient descent 來加速訓練的過程,在每一次的迭代中,我們從訓練用資料中隨機取出 100 筆資料來使用(稱為一個 batch)。
驗證模型
tf.argmax 可將向量中最大值的索引取出來,我們可以利用這個函數來檢查模型預測值與實際值是否相符合:
correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))
再將這些布林值轉換為浮點數,計算整體模型的準確度:
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
最後一步就是實際執行驗證:
print(sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))
0.9074
準確率大約在 90% 左右,這個值尚未達到收斂的值,如果多增加訓練的步驟,大概可以增加到 92% 以上。
繼續閱讀: 12



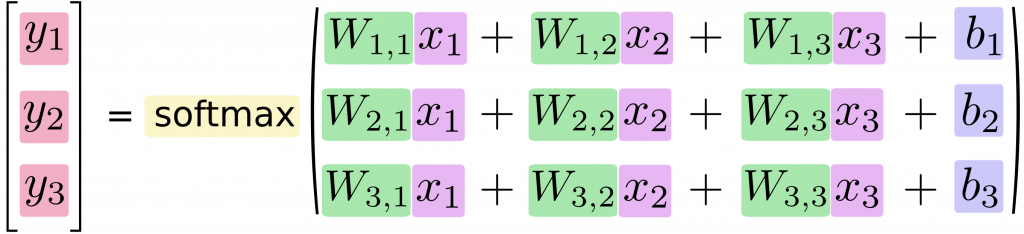
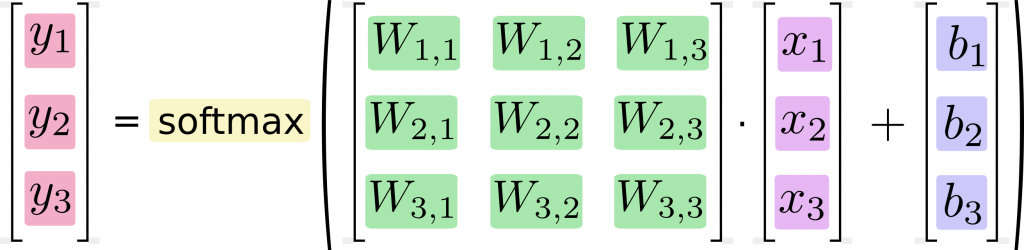
Jerry
超棒的好文~謝謝