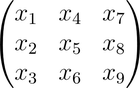Octave 算式（Expressions）

在 Octave 中算式（Expressions）是一般程式最基本的組成要件，一個算式會計算出一個值，這個值可以直接輸出、傳給判斷式做判斷、儲存在變數中、傳給函數做為輸入參數或是使用指定運算子將其指定給其他的變數。

大部分的判斷式都包含了多個算式，而一個算式也可以直接做為判斷式。Octave 的算式與其他語言類似，包含變數、陣列、常數、函數的呼叫與以上的組合。

索引算式（Index Expressions）

索引算式（Index Expressions）可以用來存取矩陣或向量中指定的元素。索引算式可以式純量、向量、範圍或是一個冒號 :（用來表示所有的行或列）。

向量是使用單一個索引算式；矩陣則可以使用單一個或兩個索引，當矩陣使用單一個索引時，則會將矩陣中的元素以行（column）優先的順序取其索，例如：

A = [1, 2, 3; 4, 5, 6; 7, 8, 9];
A(2)

輸出為

ans =  4

使用索引算式的輸出會依照索引的形式而有不同，例如上面這個範例是使用純量作為索引，則輸出亦為純量。若使用列向量的索引：

A(1:2)

則輸出為列向量

ans =

   1   4

而使用行向量的索引：

A([1; 2])

則輸出為行向量

ans =

   1
   4

若使用單一個冒號作為索引，則會傳回所有元素所組成的行向量，例如：

A(:)

輸出為

下面這三個寫法都是將矩陣 A 的第一列取出：

A(1, [1, 2, 3])
A(1, 1:3)
A(1, :)

三個寫法的輸出皆為

ans =

   1   2   3

一般來說，一個 n 維的陣列可以使用 m 個索引來存取，若 n 等於 m 時，則每一個索引會對應一個維度，這些索引（純量、向量或範圍）會以笛卡兒乘積的方式構成最後的結果；若 n 大於 m，則最後 n-m+1 維的資料會合併成一個維度，例如：

B = rand(3,2,2)

產生一個隨機的多為陣列 B，輸出為

B =

ans(:,:,1) =

   0.684732   0.407394
   0.165819   0.554558
   0.203612   0.016332

ans(:,:,2) =

   0.96476   0.83252
   0.12081   0.22859
   0.22828   0.51808

B 的維度是三，若只使用兩個維度的索引，則最後兩個維度的資料會合併成一維：

B(1,:)

輸出為

ans =

   0.68473   0.40739   0.96476   0.83252

若使用都是 1 的矩陣做為純量的索引矩陣，可以建立與索引矩陣相同大小的矩陣，而其中的值皆等於此純量值，例如：

a = 5;
a(ones(2, 3))

輸出為

也可以寫成這樣

5(ones(2, 3))

除了矩陣之外，亦可建立向量：

6(ones(1, 5))

輸出為

ans =

   6   6   6   6   6

ones(1, n) 會產生一個元素都是 1 的列向量，但其會以範圍（range）的形式傳回，因此其效率會比使用其他形式的 ones() 來的高。

當 r 是一個列向量時，下面兩個寫法所產生的結果是相同的：

r(ones (1, n), :)
r(ones (n, 1), :)

但是第一種寫法的執行效率會比較快，尤其是在 r 與 n 非常大的時候，原因在於第一種寫法會將索引向量保持在一個壓縮的狀態，這樣可以讓 Octave 選擇以更有效綠的演算法來處理。

對一般使用者而言，若不想考慮這種細微的差異，最好的方式是直接使用 repmat() 函數來處理這類的問題。

若要建立每個元素都有不同值的矩陣，可以使用迴圈配合索引：

for i = 1:10
  A(i) = sqrt (i);
endfor

這樣會建立一個矩陣 A，而第 i 個元素的值為 sqrt(i)，然而這樣使用迴圈的寫法不是很有效率，以這個例子而言可以改成下面這樣的寫法：

A = sqrt (1:10);

這樣可以避免使用迴圈，若無法避免使用迴圈時，或是要將大量的資料組成一個矩陣時，事先設定好矩陣的大小，而後再使用索引來指定矩陣中的值，可以增加執行的效率，例如：

[nr, nc] = size (a);
x = zeros (nr, n * nc);
for i = 1:n
  x(:, (i-1)*nc+1:i*nc) = a;
endfor

執行起來會比下面這個寫法快

x = a;
for i = 1:n-1
  x = [x, a];
endfor

這兩種寫法的差異在矩陣的較大時才會比較明顯，第一種寫法可以避免讓 Octave 重複改變矩陣的大小，所以執行上的效率較高。

要指定矩陣或多維的陣列的元素，可以使用多維的索引，也就是一般的下標（subscripts），例如使用一般下標的方式指定三乘三的矩陣：

$$ \begin{bmatrix} x_{11} & x_{12} & x_{13} \\ x_{21} & x_{22} & x_{23} \\ x_{31} & x_{32} & x_{33} \end{bmatrix} $$

但也可以利用一維的索引來指定其中的元素，而其排列的順序是以行為優先：

$$ \begin{bmatrix} x_1 & x_4 & x_7 \\ x_2 & x_5 & x_8 \\ x_3 & x_6 & x_9 \end{bmatrix} $$

下標與一維索引可以使用下面的函數做轉換。

ind = sub2ind (dims, i, j)
ind = sub2ind (dims, s1, s2, ..., sN)

sub2ind(dims, i, j) 函數會將下標（subscripts）轉換為一維的索引（index），例如下面這個例子會將三乘三矩陣的二維索引 (2, 3) 轉換成一維的索引：

linear_index = sub2ind ([3, 3], 2, 3)

輸出為

linear_index =  8

[s1, s2, ..., sN] = ind2sub (dims, ind)

ind2sub(dims, ind) 函數會將一維的索引（index）轉換為下標（subscripts），例如下面這個例子會將三乘三矩陣的一維索引 (2, 3) 轉換成二維的索引：

[r, c] = ind2sub ([3, 3], 8)

輸出為

r =  2
c =  3

呼叫函數（Calling Functions）

函數（function）是一個特定運算的名稱，由於其永擁有名稱，因此可以在程式中的任何地方呼叫，例如 sqrt() 是用於計算平方根的函數。

Octave 中有一系列的內建函數（built-in function），這些內建函數可以用於任何的 Octave 程式，例如 sqrt() 就是一個內建函數。另外，使用者也可以自行定義函數，關於自訂函數，請參考函數與指令稿（Functions and Scripts）。

要呼叫函數可以使用函數呼叫算，其包含函數的名稱與一連串使用括號包起來的的參數，若有一個以上的參數，則以逗號分隔，若沒有任何參數，可以省略小括號，但建議將小括號保留，這樣可以讓程式碼更容易閱讀，以下是一些呼叫函數的範例：

sqrt (x^2 + y^2)      # One argument
ones (n, m)           # Two arguments
rand ()               # No arguments

每一個函數都會接受特定個數的參數，例如 sqrt() 函數只接受一個參數，並計算此參數的平方根：

sqrt(argument)

有一些內建函數可以依據其不同的使用方式，接受不同個數的參數，而其功能也會因為輸入不同的參數而有所不同。

函數呼叫算式與一般其他的算式一樣都有傳回值，此傳回值是由此函數根據輸入的參數所運算的結果，例如 sqrt(argument) 的傳回值是 argument 的平方根。而函數有時也會有一些其他的邊際效應，例如指定一些變數的值或進行資料的輸入或輸出等。

Octave 的函數與一般程式語言的函數有一個很大的不同，Octave 的函數可以有多個傳回值，例如：

[u, s, v] = svd (a)

會計算矩陣 a 的 SVD 分解（singular value decomposition），並將計算結果儲存至 u、 s 與 v。在多重傳回值算式中，等號左邊事實上是一個逗點分隔序列，其可以是逗點分隔的變數名稱或索引算式，請參考索引算式與指定算式。

傳值呼叫（Call by Value）

Octave 中所有的函數都是使用傳值呼叫（call by value），也就是 Octave 會將函數的參數在傳入前先複製一份，在函數中所使用的值是經過複製的副本，所以改變函數中的值並不會對原來函數外的值造成影響，例如：

function f (x, n)
  while (n-- > 0)
    disp (x);
  endwhile
endfunction

這個函數會顯示 x 的值 n 次，在函數中的 n 是由函數參數中的 n 的副本，因此在函數中改變 n 的值，對於函數外的 n 並無影響。傳值呼叫的優點是使用者可以傳入一個常數至函數中，不用擔心此函數是否會改變傳入的值。

目前 Octave 不支援傳址呼叫（call by reference）。

函數在呼叫時可以使用變數名稱，但函數本身會將每個參數視為一個算式，只會將其運算值傳入函數中，例如：

foo = "bar";
fcn (foo)

函數 fcn(foo) 的參數會被視為一個字串 "bar"，而不是一個名稱為 foo 的變數。

雖然 Octave 的函數都是使用傳值呼叫，但事實上 Octave 會避免不必要的副本存在，也就是說當傳入一個值進入函數中時，若在函數中沒有改變這個值，則 Octave 會讓函數內的變數與函數外的變數使用同一份資料，避免浪費記憶體空間，例如：

x = rand (1000);
f (x);

這會將一個 1000 乘 1000 的矩陣傳入函數 f() 中，若是在 f() 函數中沒有更動 x 的值，則 Octave 就不會將 x 複製一份一樣的 x 在 f() 中，而會讓兩者共用一份資料，這樣可以節省記憶體空間，增加執行效率。

遞迴（Recursion）

在 Octave 中可以使用遞迴（Recursion）的方式來撰寫函數，例如使用遞迴的方式計算階乘（factorial）：

function retval = fact (n)
  if (n > 0)
    retval = n * fact (n-1);
  else
    retval = 1;
  endif
endfunction

這個函數是一個遞迴函數，它會自己呼叫自己，每一次呼叫自己時，會將傳入的參數 n 減去 1，直到 n 等於 0 時傳回 1。這裡定義的函數是為了示範遞迴函數的使用方式，若是要計算階乘可以使用較有效率的 prod(1:n) 或 gamma(n+1)。

val = max_recursion_depth ()
old_val = max_recursion_depth (new_val)

max_recursion_depth() 函數可以查詢或設定函數遞迴呼叫的最大次數，若是遞迴呼叫的次數大於此數值，則會產生錯誤訊息，並回到最上一層。

在 Octave 中有一些函數不能使用遞迴的方式，例如 lsode() 函數是以 Fortran 語言所寫成的，其無法以遞迴呼叫的方式使用，否則會產生錯誤。

算數運算子（Arithmetic Operators）

Octave 中的算術運算子（Arithmetic Operators）可以用於純量或矩陣：

x + y：加法，若 x 與 y 皆為矩陣，則兩個矩陣必須有相同的大小，若一個是純量另一個是矩陣，則會將矩陣中每一個元素與純量相加。
x .+ y：元素加法，此運算子與 +. 相同。
x - y：減法，若 x 與 y 皆為矩陣，則兩個矩陣必須有相同的大小，若一個是純量另一個是矩陣，則會將矩陣中每一個元素與純量相減。
x .- y：元素減法，此運算子與 -. 相同。
x * y：乘法，若 x 與 y 皆為矩陣，則 x 的行數必須等於 y 的列數。
x .* y：元素乘法，若 x 與 y 皆為矩陣，則兩個矩陣必須有相同的大小。
x / y：右除法，其作用相當於 (inverse (y') * x')'，但其不需要計算 y'。若係數矩陣不是方陣或為 singular，則會計算 minimum norm solution。
x ./y：元素右除法。
x y：左除法，其作用相當於 inverse (x) * y，但不需要計算 inverse(x)。若係數矩陣不是方陣或為 singular，則會計算 minimum norm solution。
x . y：元素左除法，y 中的每個元素會除以 x 中所對應的元素。
x ^ y 與 x ** y：指數，若 x 與 y 皆為純量，則傳回 x 的 y 次方；若 x 為純量，y 為方陣，則會使用 eigenvalue expansion 計算結果；若 x 為方陣，y 為一個整數，則會傳回 x 連續 y 次乘積的結果（若 y 不是整數，則會使用 eigenvalue expansion）；若 x 與 y 皆為矩陣，則會產生錯誤。
x .^ y 與 x .** y：元素指數，若 x 與 y 皆為矩陣，則兩個矩陣必須有相同的大小。
-x：負數。
+x：正數，這個運算子基本上沒作用。
x'：共軛轉置（conjugate transpose），對於實數而言，這個運算子等同於轉置（transpose）運算子，而對於複數，此運算子等同於 conj (x.')。
x.'：轉置（transpose）。

由於 Octave 的元素運算子是以小數點開頭，因此在使用時有可能會發生一些模稜兩可的情況，例如：

1./m

因為這個小數點可以被解釋為常數 1 的小數點或是元素右除法，為了避免混淆，Octave 碰到這種情況會把他解釋為

(1) ./ m

而不是

(1.) / m

比較運算子（Comparison Operators）

比較運算子（Comparison Operators）可以比較兩個數值之間的關係，所有 Octave 的比較運算子在結果是 true 時會傳回 1，而結果是 false 時則傳回 0，若傳入值為矩陣，則會對矩陣中的每個元素進行比較，例如：

[1, 2; 3, 4] == [1, 3; 2, 4]

輸出為

若有一個運算元是矩陣而另外一個是純量，則會將此純量依序與矩陣中的元素進行比較，其傳回值為一個與運算元矩陣相同大小的矩陣。以下是一些 Octave 中的比較運算子：

x < y：判斷 x 是否小於 y。
x <= y：判斷 x 是否小於或等於 y。
x == y：判斷 x 是否等於 y。
x >= y：判斷 x 是否大於或等於 y。
x > y：判斷 x 是否大於 y。
x != y 與 x ~= y：判斷 x 是否不等於 y。

這些運算子是用於數值間的比較，無法用於字串，字串之間的比較可以使用 strcmp() 函數，請參考字串資料。

isequal (x1, x2, ...)

isequal(x1, x2, ...) 函數會判斷 x1, x2, ... 是否相等。

isequalwithequalnans (x1, x2, ...)

isequalwithequalnans(x1, x2, ...) 函數會在 NaN == NaN 的判斷條件下，判斷 x1, x2, ... 是否相等。

布林算式（Boolean Expressions）

元素對元素布林算式（Element-by-element Boolean Operators）

元素對元素布林算式（element-by-element boolean operators）是指使用元素對元素布林運算子（element-by-element boolean operators）與小括號將比較算式連接起來的算式，布林運算子包含：and（&）、or（|）與 not（!），而小括號是用於控制計算的優先順序。布林算式的運算結果是由其中的比較算式的結果再經由布林運算子運算而得到，若結果為 true 則傳回 1，否則傳回 0。

在任何比較算式可以使用的地方也都可以使用元素對元素布林算式，例如 if 或 while 判斷式中都可以使用元素對元素布林算式。

在 if 與 while 等判斷式中使用矩陣時，若矩陣中所有的元素皆不為 ``，則傳回 true，否則傳回 false。

若將元素對元素布林算式用於數值運算或儲存至變數中，當其運算結果為 true 時，其傳回值為 1，而結果為 false 時，其傳回值為 0。例如：

a = 1;
b = 2;
c = (a < 2) & (b > 1)

輸出為

c =  1

以下是 Octave 中的元素對元素布林運算子：

boolean1 & boolean2：將 boolean1 與 boolean2 中對應的元素做 AND 運算。
boolean1 | boolean2：將 boolean1 與 boolean2 中對應的元素做 OR 運算。
! boolean：對 boolean 中每個元素做 NOT 運算。
~ boolean：與 ! boolean 相同。

若輸入的運算元為矩陣為矩陣，則會對每個元素做運算，例如：

[1, 0; 0, 1] & [1, 0; 2, 3]

輸出為

對於二元的元素對元素布林運算子（即 & 與 |），若兩個運算元（也就是上面的 boolean1 與 boolean2）皆為矩陣，則兩個矩陣的大小必須相同；若一個運算元為純量，而另一個是矩陣，則會以純量對每個矩陣中的元素做運算。

由二元的元素對元素布林運算子所連接的算式（即上面的 boolean1 與 boolean2）會在計算結果之前先被執行，這在元素對元素布林算式含有邊際效應時會產生差異，例如：

a & b++

即使 a 的值為 0，b 依然會遞增。

短路布林運算子（Short-circuit Boolean Operators）

Octave 所提供的元素對元素布林運算子配合其自動轉換為數值的特性，對於大部分的情況而言已經足夠了，但有時候使用者會希望當運算結果已經確定時，可以跳過不需要的運算，短路布林運算子（Short-circuit Boolean Operators）就是為了這個而設計的：

boolean1 && boolean2：boolean1 算式會以 all (boolean1(:)) 的方式檢查其是否為 true，若為 false 則不執行 boolean2，整個算式會傳回 0；若 boolean1 為 true，則 boolean2 算式會以 all (boolean2(:)) 的方式檢查其是否為 true，若為 true 則整個算式會傳回 1，否則傳回 0。
boolean1 || boolean2：boolean1 算式會以 all (boolean1(:)) 的方式檢查其是否為 true，若為 true 則不執行 boolean2，整個算式會傳回 1；若 boolean1 為 false，則 boolean2 算式會以 all (boolean2(:)) 的方式檢查其是否為 true，若為 true 則整個算式會傳回 1，否則傳回 0。

當 boolean1 為空矩陣時，使用 all (boolean1(:)) 時有一個例外，即使 all ([]) 為 true，但 [] && true 依然為 false。

短路布林運算子所連接的算式有可能不會被直行，例如：

a && b++

只有當 a 不是 0 時，b 才會遞增。

善用短路布林運算子的特性可以讓程式碼更簡潔，例如：

function f (a, b, c)
  if (nargin > 2)
    if (ischar (c))
      ...

可以使用短路布林運算子改寫成：

function f (a, b, c)
  if (nargin > 2 && ischar (c))
    ...

若是寫成

function f (a, b, c)
  if (nargin > 2 & ischar (c))
    ...

則在 f() 函數只有輸入一個或兩個參數時，會產生錯誤，因為 & 運算子會先執行其兩邊的運算元。

指定算式（Assignment Expressions）

指定算式（Assignment Expressions）是將一個值指定給一個變數，例如將一個數值 1 指定給變數 z：

z = 1

執行這個算式之後，變數 z 的原本的值會被 1 取代，這裡的等號（=）稱為指定運算子。指定算式亦可指定字串，例如：

s = "test string"

大部分的運算子（例如加法運算子）只會根據運算元計算一個傳回值，而不會改變運算元原本的值，若是忽略其傳回值，則運算元等於沒有作用，但指定運算子則不同，即便忽略其傳回值，他還是會改變變數中的值，這個稱為運算子的邊際效應（side effect）。

指定運算子的左邊可以是變數（請參考變數）、矩陣的元素（請參考索引算式）或傳回值的逗點分隔序列（請參考呼叫函數），這些統稱作 lvalue，意思是這些都可以放在指定運算子的左邊；而在指定運算子的右邊則可以是任何的算式，這個算式所產生的值會被指定為指定運算子左邊的變數、矩陣元素或逗點分隔序列的值。

在 Octave 中的變數並沒有固定的資料類型，變數的類型是依據其目前所儲存的資料而定，例如：

foo = 1
foo = "bar"

第一行算式將變數 foo 指定為數值 1，而第二行將 foo 指定為字串 "bar" 時，之前的數值就會被覆蓋掉。

若將一個純量指定給矩陣中的一部分元素，則會將每個元素指定為此純量的值，例如：

A = ones(3);
A(:, 2) = 5

這會將矩陣 A 第二行的每一個元素都指定為 5，輸出為：

若指定為空矩陣，則可以刪除矩陣的行或列（請參考矩陣），例如：

A = [1, 2; 3, 4; 5, 6];
A (2, :) = []

這會將矩陣 A 的第二列刪除，輸出為

A = [1, 2, 3, 4, 5; 6, 7, 8, 9, 10; 11, 12, 13, 14, 15];
A(:, 1:2:5) = []

這會將矩陣 A 的第一、三、五列刪除，輸出為

指定算式也有傳回值，例如 z = 1 的傳回值就是 1，使用這個特性可以將多個指定算式合併成一個：

x = y = z = 0

這個算式首先將 z 設為 0，而後將 z = 0 的傳回值（其值為 0）設定給 y，最後將 y = z = 0 的傳回值（其值為0）設定給 x，所以最後 x、y 與 z 皆被設為0。這樣的寫法也可以用於逗點分隔序列，例如：

[a, b, c] = [u, s, v] = svd (a)

這樣的寫法等同於

[u, s, v] = svd (a)
a = u
b = s
c = v

使用這樣的寫法，每個逗點分隔序列不需要有相同個數的變數，例如：

[a, b] = [u, s, v] = svd (a)

這樣的寫法也是可以的，其作用等同於

[u, s, v] = svd (a)
a = u
b = s

位於指定運算子左邊的逗點分隔序列的變數個數不可以多於右邊的個數，否則會產生錯誤，例如：

[a, b, c, d] = [u, s, v] = svd (a);

這樣 Octave 就會產生錯誤：

error: element number 4 undefined in return list

在一般程式設計中有一個很常用的算式就是將某個變數加上一個數值，例如將變數 x 加上 2：

x = x + 2;

這種算式可以使用 += 運算子改寫成更精簡的寫法：

x += 2;

類似的用法也可以用於其他的運算子上：

一般用法	簡潔用法
`x = x + 2`	`x += 2`
`x = x - 2`	`x -= 2`
`x = x * 2`	`x *= 2`
`x = x / 2`	`x /= 2`

a *= b + 1 是等同於 a = a * (b + 1) 不是 a = a * b + 1。

指定算式可以用於任何一般算式可以使用的地方，例如 x != (y = 1) 會將 y 指定為 1 並測試 x 是否不等於 1，雖然 Octave 允許這樣的寫法，但這樣寫會造成程式閱讀上的困難，除非是用於只使用一次的程式，否則最好避免以這種不好閱讀的方式撰寫程式。

遞增運算子（Increment Operators）

遞增運算子（Increment Operators）可以將變數的值增加 1 或減少 1，其使用方式與 C 語言中的遞增運算子相同，以下是 Octave 中的遞增運算子：

++x：將 x 的值加 1，傳回增加後的數值。
--x：將 x 的值減 1，傳回增加後的數值。
x++：將 x 的值加 1，傳回增加前的數值。
x--：將 x 的值減 1，傳回增加前的數值。

++x 會先將變數 x 的值加 1 後，再取其新的值傳回，其作用完全等於 x = x + 1。而 x++ 則是將變數 x 的值加 1 後，傳回原本舊的數值；而 --x 與 x-- 的差異也是類似。例如：

x = 1;
y = ++x;

此時的 x 為 2，而 y 為 2，

x = 1;
y = x++;

此時的 x 為 2，而 y 為 1。

遞增運算子與一個變數所組成的算式與一般的算式相同，可以用於任何其他算式可以使用的地方，例如判斷式之中：

a = b = 1;
a++ > b

輸出為

ans = 0

運算子優先權（Operator Precedence）

當算式中包含多個運算子時，運算子優先權（operator precedence）會決定其運算的順序，例如乘法運算子 * 都優先順序就會比加法運算子 + 高，因此 a + b * c 的運算順序是先將 b 乘以 c 再加上 a，也就是 a + (b * c)。

使用者可以使用小括號更改預設的運算子優先權，此優先權亦可視為當使用者沒有使用括號時，預設的括號規則。當在使用一些不常見的運算子組合時，縱使依照預設的運算子優先權可以不需要括號，但一般還是建議加入小括號，因為不是每個閱讀程式的人都記得每個運算子的優先順序，有明確的括號可以避免不必要的錯誤發生。

一般當兩個運算子有相同的優先權時，在左邊的運算子會先執行。指定運算子（assignment operator）與指數運算子（exponentiation operator）與一般運算子不同，這兩種運算子會由最右邊的運算子開始執行，例如 a - b + c 其運算順序為 (a - b) + c，而 a = b = c 的運算順序則為 a = (b = c)。

運算子的優先權對於前置的一元運算子（prefix unary operators）是很重要的，例如：-x^2 的執行順序為 -(x^2)，這是因為負號 - 的優先順序低於指數運算子 ^。

以下是 Octave 中各種運算子的優先順序，依照由低而高的順序排列：

分隔符號（statement separators）：";"、 ","。
指定運算子（assignment）："="、 "+="、 "-="、 "*="、 "/="，這些運算子是由最右邊開始執行。
短路布林運算子 OR 與 AND："||"、 "&&"。
元素對元素布林運算子 OR 與 AND："|"、 "&"。
比較運算子："<"、 "<="、 "=="、 ">="、 ">"、 "!="、 "~="。
冒號運算子：":"。
加法與減法運算子："+"、 "-"。
乘法與除法運算子："*"、 "/"、 ""、 "."、 ".*"、 "./"。
轉置（transpose）："'"、 ".'"。
一元運算子："+"、 "-"、 "++"、 "--"、 "!"、 "~"。
指數運算子（exponentiation）："^"、 "**"、 ".^"、 ".**"。

索引算式（Index Expressions）#

呼叫函數（Calling Functions）#

傳值呼叫（Call by Value）#

遞迴（Recursion）#

算數運算子（Arithmetic Operators）#

比較運算子（Comparison Operators）#

布林算式（Boolean Expressions）#

元素對元素布林算式（Element-by-element Boolean Operators）#

短路布林運算子（Short-circuit Boolean Operators）#

指定算式（Assignment Expressions）#

遞增運算子（Increment Operators）#

運算子優先權（Operator Precedence）#