公式
R 的公式(formula)是一種特殊的語法,用來表示由變數所構成的模型,至於實際上所代表的意義則會跟使用模型的函數有關。
我們以 iris 這個 R 內建的資料集做示範,假設我們有一個迴歸模型如下:
[begin{aligned}
mbox{Sepal.Length} = & beta_0+beta_1*mbox{Sepal.Width}+
& beta_2*mbox{Petal.Width}+beta_3*mbox{Petal.Length}+epsilon
end{aligned}]
若使用 R 的公式表示則為:
Sepal.Length ~ Sepal.Width + Petal.Width + Petal.Length
公式的左側是擺放反應變數(response variable)而右側則是放解釋變數(explanatory variables),中間以一個 ~ 符號區隔,而右側若有多個解釋變數,則使用加號 + 分隔,這樣就是一個最簡單的線性模型。
若要指定沒有截距項的模型:
[begin{aligned}
mbox{Sepal.Length} = & beta_1*mbox{Sepal.Width}+
& beta_2*mbox{Petal.Width}+beta_3*mbox{Petal.Length}+epsilon
end{aligned}]
則可以在右側加上一個 0,這樣就代表不包含截距項的模型:
Sepal.Length ~ 0 + Sepal.Width + Petal.Width + Petal.Length
下表是常用於 R 公式中的各種符號與意義。
| 符號 | 意義 |
|---|---|
~ |
分隔反應變數(左側)與解釋變數(右側)。 |
+ |
分隔多個解釋變數。 |
: |
代表解釋變數之間的交互作用,例如 y ~ x + z + x:z 就代表除了以 x 與 z 解釋 y 之外,還加入了 x 與 z 兩個變量的交互作用。 |
* |
代表所有可能的交互作用,例如 y ~ x * z * w 就等同於 y ~ x + z + w + x:z + x:w + z:w + x:z:w。 |
^ |
以次方表示變數之間的交互作用,例如 y ~ (x + z + w)^2 就等同於 y ~ x + z + w + x:z + x:w + z:w。 |
. |
代表除了反應變數之外,data frame 中所有的變數,假設整個 data frame 中包含 x、y、z 與 w ,則 y ~ . 就代表 y ~ x + z + w。 |
- |
減號代表從現有的模型中移除指定的解釋變數,例如 y ~ (x + z + w)^2 – x:w 就代表 y ~ x + z + w + x:z + z:w。 |
-1 |
移除截距項,例如 y ~ x - 1。 |
+0 |
移除截距項,與 -1 相同,例如 y ~ x + 0 或 y ~ 0 + x。 |
I() |
以數學意義解釋,例如一般的 y ~ x + (z + w)^2 會等同於 y ~ x + z + w + z:w,而 y ~ x + I((z + w)^2) 則會等同於 y ~ x + h,其中這個 h 是一個新建立的變數,其值為 z 與 w 總和的平方,亦即 (h = (z + w)^2)。 |
| 一般函數 | 一般的數學函數都可以直接用在公式中,例如 log(y) ~ x + z + w。 |
線性迴歸模型
線性迴歸模型是最簡單的迴歸模型,它可以使用公式指定迴歸模型,並指定資料來源的 data frame,例如:
iris.lm <- lm(Petal.Width ~ Petal.Length, data = iris) iris.lm
Call:
lm(formula = Petal.Width ~ Petal.Length, data = iris)
Coefficients:
(Intercept) Petal.Length
-0.3631 0.4158
這樣就完成最簡單的線性迴歸模型配適。
以 lm 配適所得到的結果,可以使用以下這些函數來顯示更詳細的資訊,或做進一步的分析:
| 函數 | 功能 |
|---|---|
summary() |
顯示詳細的模型配適結果。 |
coefficients() |
顯示模型的迴歸係數,包含截距項與各解釋變數的係數。 |
confint() |
計算迴歸係數的區間估計值,預設會計算 95% 的信賴區間。 |
fitted() |
根據模型計算配適值。 |
residuals() |
根據模型計算殘差值。 |
anova() |
計算變異數分析(ANOVA)表格。 |
vcov() |
計算模型參數的變異數矩陣(covariance matrix)。 |
AIC() |
計算模型的 AIC(Akaike’s Information Criterion)值。 |
plot() |
畫出模型診斷用的各種圖形。 |
predict() |
以配適出來的模型,對新的資料進行預測。 |
coefficients 可顯示配適出來的迴歸係數:
coefficients(iris.lm)
(Intercept) Petal.Length -0.3630755 0.4157554
使用 summary 可以顯示更詳細一點的資訊:
summary(iris.lm)
Call:
lm(formula = Petal.Width ~ Petal.Length, data = iris)
Residuals:
Min 1Q Median 3Q Max
-0.56515 -0.12358 -0.01898 0.13288 0.64272
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.363076 0.039762 -9.131 4.7e-16 ***
Petal.Length 0.415755 0.009582 43.387 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.2065 on 148 degrees of freedom
Multiple R-squared: 0.9271, Adjusted R-squared: 0.9266
F-statistic: 1882 on 1 and 148 DF, p-value: < 2.2e-16
列出模型的配適值:
head(iris$Petal.Width)
1 2 3 4 5 6 0.2189821 0.2189821 0.1774065 0.2605576 0.2189821 0.3437087
與實際值做比較:
head(fitted(iris.lm))
[1] 0.2 0.2 0.2 0.2 0.2 0.4
列出殘差值:
head(residuals(iris.lm))
1 2 3 4 5 6 -0.01898206 -0.01898206 0.02259348 -0.06055760 -0.01898206 0.05629131
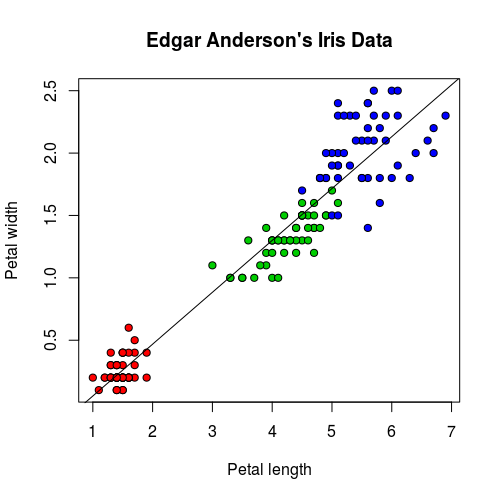
對於變數不多的模型,我們可以畫出其迴歸線與資料的圖形:
plot(iris$Petal.Length, iris$Petal.Width, pch=21, bg = c("red", "green3", "blue")[unclass(iris$Species)], main = "Edgar Anderson's Iris Data", xlab = "Petal length", ylab="Petal width") abline(iris.lm$coefficients, col = "black")
有時候基本的線性模型可能會無法準確地解釋資料,我們來看 Sepal.Length 與 Sepal.Width 之間的關係:
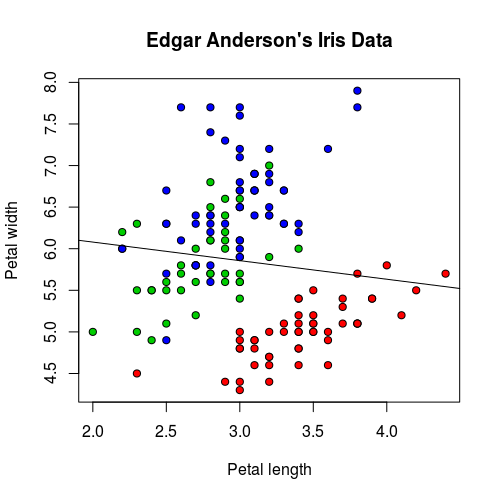
iris.lm2 <- lm(Sepal.Length ~ Sepal.Width, data = iris) plot(iris$Sepal.Width, iris$Sepal.Length, pch=21, bg = c("red", "green3", "blue")[unclass(iris$Species)], main = "Edgar Anderson's Iris Data", xlab = "Petal length", ylab="Petal width") abline(iris.lm2$coefficients, col = "black")
這是 Sepal.Length 與 Sepal.Width 的迴歸線,直接從圖形上看起來就可以發現這個模型配適的不太好。
若從 p-value 來看,結果也是一樣不好:
summary(iris.lm2)
Call:
lm(formula = Sepal.Length ~ Sepal.Width, data = iris)
Residuals:
Min 1Q Median 3Q Max
-1.5561 -0.6333 -0.1120 0.5579 2.2226
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.5262 0.4789 13.63
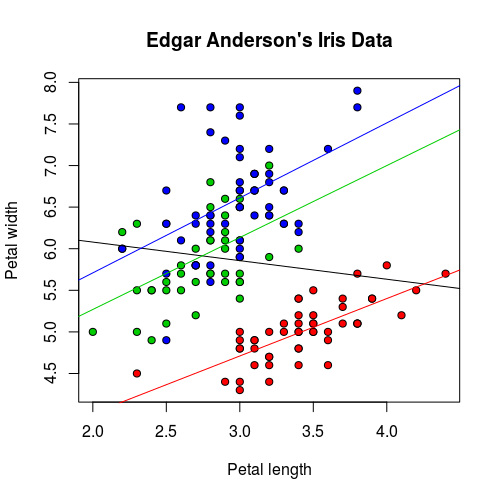
這種狀況若將資料依據 Species 分組,再使用迴歸線配適,結果就會比較好:
iris.lm2 <- lm(Sepal.Length ~ Sepal.Width, data = iris) iris.setosa.lm2 <- lm(Sepal.Length ~ Sepal.Width, data = iris[which(iris$Species=="setosa"),]) iris.versicolor.lm2 <- lm(Sepal.Length ~ Sepal.Width, data = iris[which(iris$Species=="versicolor"),]) iris.virginica.lm2 <- lm(Sepal.Length ~ Sepal.Width, data = iris[which(iris$Species=="virginica"),]) plot(iris$Sepal.Width, iris$Sepal.Length, pch=21, bg = c("red", "green3", "blue")[unclass(iris$Species)], main = "Edgar Anderson's Iris Data", xlab = "Petal length", ylab="Petal width") abline(iris.lm2$coefficients, col = "black") abline(iris.setosa.lm2$coefficients, col = "red") abline(iris.versicolor.lm2$coefficients, col = "green3") abline(iris.virginica.lm2$coefficients, col = "blue")
這樣三組資料所配適的模型都相當顯著。
summary(iris.setosa.lm2)
Call:
lm(formula = Sepal.Length ~ Sepal.Width, data = iris[which(iris$Species ==
"setosa"), ])
Residuals:
Min 1Q Median 3Q Max
-0.52476 -0.16286 0.02166 0.13833 0.44428
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.6390 0.3100 8.513 3.74e-11 ***
Sepal.Width 0.6905 0.0899 7.681 6.71e-10 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.2385 on 48 degrees of freedom
Multiple R-squared: 0.5514, Adjusted R-squared: 0.542
F-statistic: 58.99 on 1 and 48 DF, p-value: 6.71e-10
summary(iris.versicolor.lm2)
Call:
lm(formula = Sepal.Length ~ Sepal.Width, data = iris[which(iris$Species ==
"versicolor"), ])
Residuals:
Min 1Q Median 3Q Max
-0.73497 -0.28556 -0.07544 0.43666 0.83805
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.5397 0.5629 6.289 9.07e-08 ***
Sepal.Width 0.8651 0.2019 4.284 8.77e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.4436 on 48 degrees of freedom
Multiple R-squared: 0.2766, Adjusted R-squared: 0.2615
F-statistic: 18.35 on 1 and 48 DF, p-value: 8.772e-05
summary(iris.virginica.lm2)
Call:
lm(formula = Sepal.Length ~ Sepal.Width, data = iris[which(iris$Species ==
"virginica"), ])
Residuals:
Min 1Q Median 3Q Max
-1.26067 -0.36921 -0.03606 0.19841 1.44917
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.9068 0.7571 5.161 4.66e-06 ***
Sepal.Width 0.9015 0.2531 3.562 0.000843 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.5714 on 48 degrees of freedom
Multiple R-squared: 0.2091, Adjusted R-squared: 0.1926
F-statistic: 12.69 on 1 and 48 DF, p-value: 0.0008435
像上面這樣將資料分組之後,再進行配適的模型,可以使用這樣的公式表示:
Sepal.Length ~ Sepal.Width:Species + Species - 1
使用 lm 配適的結果完全相同:
iris.lm3 <- lm(Sepal.Length ~ Sepal.Width:Species + Species - 1, data = iris) iris.lm3
Call:
lm(formula = Sepal.Length ~ Sepal.Width:Species + Species - 1,
data = iris)
Coefficients:
Speciessetosa Speciesversicolor Speciesvirginica
2.6390 3.5397 3.9068
Sepal.Width:Speciessetosa Sepal.Width:Speciesversicolor Sepal.Width:Speciesvirginica
0.6905 0.8651 0.9015
由於 Species 是類別型的資料(R 的因子變數),無法直接用於迴歸模型的中,所以 R 會自動依據 Species 建立一些虛擬變數(dummy variables),讓它可以被用於迴歸模型中:
Speciessetosa:若Species為setosa則其值為1,否則為0。Speciesversicolor:若Species為versicolor則其值為1,否則為0。Speciesvirginica:若Species為virginica則其值為1,否則為0。Sepal.Width:Speciessetosa:若Species為setosa則其值為Sepal.Width,否則為0。Sepal.Width:Speciesversicolor:若Species為versicolor則其值為Sepal.Width,否則為0。Sepal.Width:Speciesvirginica:若Species為virginica則其值為Sepal.Width,否則為0。
使用 summary 顯示詳細的結果:
summary(iris.lm3)
Call:
lm(formula = Sepal.Length ~ Sepal.Width:Species + Species - 1,
data = iris)
Residuals:
Min 1Q Median 3Q Max
-1.26067 -0.25861 -0.03305 0.18929 1.44917
Coefficients:
Estimate Std. Error t value Pr(>|t|)
Speciessetosa 2.6390 0.5715 4.618 8.53e-06 ***
Speciesversicolor 3.5397 0.5580 6.343 2.74e-09 ***
Speciesvirginica 3.9068 0.5827 6.705 4.25e-10 ***
Sepal.Width:Speciessetosa 0.6905 0.1657 4.166 5.31e-05 ***
Sepal.Width:Speciesversicolor 0.8651 0.2002 4.321 2.88e-05 ***
Sepal.Width:Speciesvirginica 0.9015 0.1948 4.628 8.16e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.4397 on 144 degrees of freedom
Multiple R-squared: 0.9947, Adjusted R-squared: 0.9944
F-statistic: 4478 on 6 and 144 DF, p-value: < 2.2e-16
迴歸模型選擇
撰寫中…
參考資料:Peter Cock、Introduction to Multiple Linear Regression in R
繼續閱讀: 12