本篇為史丹佛大學機器學習（Machine Learning）課程 Lecture 3 的後半段筆記，接續 Lecture 3 前半部的內容。
Lecture 3 的線上課程錄影可以從 YouTube 網站上觀看。
接下來我們要開始介紹分類的問題，這種問題跟迴歸類似，只不過在這裡的 \(y\) 是離散的（discrete）值，而在這裡我們先討論二元分類（binary classification）的問題，也就是 \(y\) 的值只會有兩種（也就是 0 與 1）的狀況，而這邊所講述的概念大部份都可以拓展到多元分類的問題上。
舉個例子來說，如果你想要建立一個垃圾信件的篩選器，那麼 \(x^{(i)}\) 就會是一些電子郵件的特徵，而 \(y\) 的值就是 1 或 0（分別代表該郵件是否為垃圾郵件），這裡的 0 也稱為 negative class，而 1 也稱為 positive class，有時候也用加號（+）與減號（-）表示。在給定 \(x^{(i)}\) 的情況下，對應的 \(y^{(i)}\) 也稱為該 training example 的 label。
當然我們也可以不管 \(y\) 是否為離散的變數，直接使用一般的迴歸分析來處理，在一些很特殊的狀況下可能還是可以處理的不錯，例如我們的資料很規則，像下面這張圖這樣，那麼經過迴歸配適之後，我們可以把預測出來的 \(y\) 值用 0.5 來區分，超過 0.5 就視為 1，小於 0.5 則視為 0，在這個例子中可能沒有太大的問題。
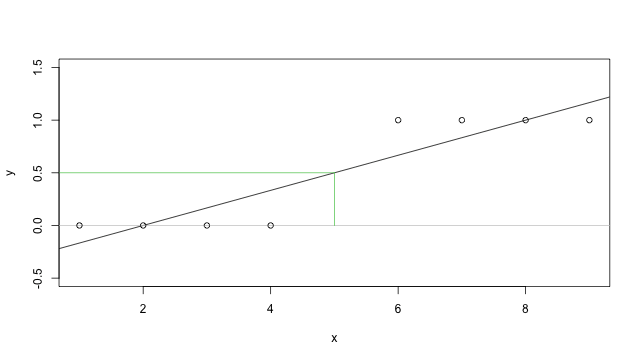
但是實際上我們可以很容易就找到一個沒辦法這樣使用的例子，例如上面這個例子我們加上一些 \(x\) 比較大的資料，就會變成下面這樣：
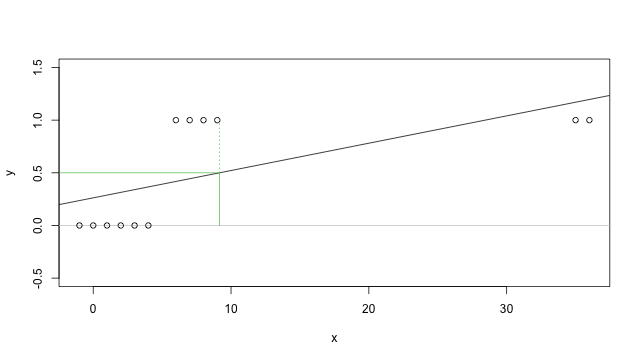
這時候你就會發現用傳統迴歸的方法，配適出來的迴歸線如果還是使用 0.5 為分界的話，就會出現一些問題（中間四筆資料的分類就會是不正確的）。
另外在直覺上，因為我們的 \(y\) 只會有兩種值（\(y \in \{0,1\}\)），如果 \(h_{\theta}(x)\) 出現大於 1 或小於 0 的值，在解釋上也不太合理。
為了解決這樣的問題，我們將 hypotheses \(h_{\theta}(x)\) 改為
\[h_{\theta}(x)=g(\theta^Tx)=\frac{1}{1+e^{-\theta^Tx}}\]
其中
\[g(z)=\frac{1}{1+e^{-z}}\]
稱為羅吉斯函數（logistic function）或 sigmoid function，下面這張圖是這個函數的長相
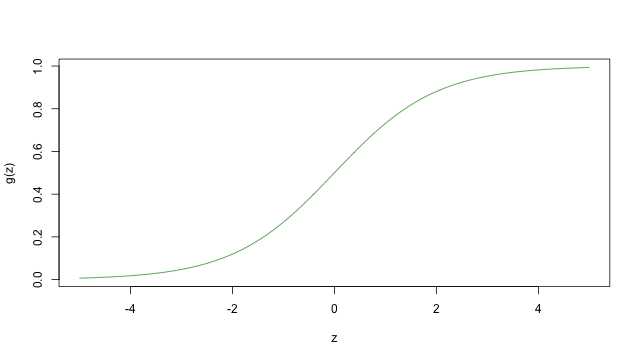
當 \(z\) 趨近於無限大（\(\infty\)）時，這個 \(g(z)\) 就會趨近於 1，而當 \(z\) 趨近於負的無限大（\(-\infty\)）時，\(g(z)\) 就會趨近於 0，由於這個性質也使得 \(h(x)\) 的值域都介於 0 與 1 之間。仿照之前的做法，令 \(x_0=1\)，我們可以得到 \(\theta^Tx=\theta_0+\sum_{j=1}^n\theta_jx_j\)。
這裡我們是直接使用 \(g\) 這個函數來作為 hypotheses 函數，而除此之外其實任何會從 0 平滑上升到 1 的函數也都可以拿來使用，之所以選擇 \(g\) 的原因在於它具有一些很自然的性質（在之後當我們討論到 GLM 與 generative learning algorithms 時就會看到）。
\(g\) 的微分有一些不錯的性質，這裡先推導一下，之後會用到：
\begin{aligned}
g'(z)=&\frac{d}{dz}\frac{1}{1+e^{-z}}\\
=&\frac{1}{(1+e^{-z})^2}\big(e^{-z}\big)\\
=&\frac{1}{1+e^{-z}} \cdot \Big(1-\frac{1}{1+e^{-z}}\Big)\\
=&g(z)(1-g(z))
\end{aligned}
之前在討論一般的迴歸模型時，我們加入了一些統計上的假設，導出最小平方迴歸就是最大概似估計，這裡也是使用類似的方法。首先假設
\begin{aligned}
P(y=1\mid x;\theta)=&h_\theta(x)\\
P(y=0\mid x;\theta)=&1-h_\theta(x)\\
\end{aligned}
而這兩個式子可以合併為
\[p(y\mid x;\theta)=(h_\theta(x))^y(1-h_\theta(x))^{1-y}\]
假設所有 \(m\) 個 training examples 都是獨立的，我們可以得到 \(\theta\) 的概似函數
\begin{aligned}
L(\theta)&=p(\vec{y}\mid X;\theta)\\
&=\prod_{i=1}^mp(y^{(i)}\mid x^{(i)};\theta)\\
&=\prod_{i=1}^m(h_\theta(x^{(i)}))^{y^{(i)}}(1-h_\theta(x^{(i)}))^{1-y^{(i)}}
\end{aligned}
跟之前的做法類似，經過對數轉換之後，就可以很容易找到它的極大值
\begin{aligned}
l(\theta)=&\log L(\theta)\\
=&\sum_{i=1}^my^{(i)}\log h(x^{(i)})+(1-y^{(i)})\log(1-h(x^{(i)}))
\end{aligned}
跟之前一般迴歸的做法一樣，我們可以使用 gradient ascent，如果以向量的形式來表示，遞迴式可以寫成 \(\theta := \theta+\alpha\nabla_{\theta}l(\theta)\)。因為在這裡我們要找的是最大值，所以在遞迴式中變動項要取成正的（跟之前迴歸的狀況相反）。
接著我們來看只有一組 training example \((x,y)\) 的情況，以及推導出來的遞迴式。
\begin{aligned}
\frac{\partial}{\partial\theta_j}l(\theta)=&\Big(y\frac{1}{g(\theta^Tx)}-(1-y)\frac{1}{1-g(\theta^Tx)}\Big)\frac{\partial}{\partial\theta_j}(\theta^Tx)\\
=&\Big(y\frac{1}{g(\theta^Tx)}-(1-y)\frac{1}{1-g(\theta^Tx)}\Big)g(\theta^Tx)(1-g(\theta^Tx)\frac{\partial}{\partial\theta_j}\theta^Tx\\
=&\big(y(1-g(\theta^Tx))-(1-y)g(\theta^Tx)\big)x_j\\
=&(y-h_\theta(x))x_j
\end{aligned}
這裡帶入剛剛上面推導過的 \(g'(z)=g(z)(1-g(z))\)，所以可以得到
\[\theta_j:=\theta_j+\alpha\big(y^{(i)}-h_\theta(x^{(x)})\big)x_j^{(i)}\]
這個結果如果跟之前的 LMS（least mean squares）演算法所推導出來的遞迴公式比較，你會發現它們是完全一樣的，但他們其實是不一樣的演算法，因為現在這裡的 \(h_\theta(x^{(i)})\) 跟之前不同，它在這裡被定義為一個非線性的函數 \(\theta^Tx^{(i)}\)。而不管怎麼樣，我們以不一樣的演算法與不同的問題，卻推導出相同的遞迴式，確實讓人有點驚訝，這到底是巧合還是另有原因，這個我們在之後討論到 GLM 的時候會來解釋。
這裡補充一個相關的演算法，這個演算法在之後講到學習理論時還會再拿來討論。假設我們把上面的羅吉斯迴歸改變一下，讓它的值只會出現 0 與 1，以也就是把 \(g(z)\) 的定義改為一個定限函數（threshold function）
\[
g(z) = \begin{cases}
1 & \mbox{if $z \geq 0$}\\
0 & \mbox{if $z < 0$}
\end{cases}
\]
跟之前一樣令 \(h_\theta(x)=g(\theta^Tx)\)，這樣也可以得到相同的遞迴式
\[\theta_j:=\theta_j+\alpha\big(y^{(i)}-h_\theta(x^{(x)})\big)x_j^{(i)}\]
這個就稱為感知學習演算法（perceptron learning algorithm）。
在 1960 年代，大家曾經爭論過感知學習演算法是否可以描述腦神經的運作，而這種簡單的演算法也可以作為這堂課的一個暖身，雖然它的樣子跟上面演算法都很相似，但它跟羅吉斯迴歸與一般的線性迴歸是完全不一樣的，尤其這種感知學習演算法無法用合理的機率理論來解釋，也沒辦法使用最大概似估計的方式推導。
